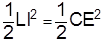1. LIGNE INFINIE
1.1. NOTION DE LONGUEUR D’ONDE
La longueur d’onde (l) est la distance parcourue par l’énergie pendant une période du signal débité par le générateur l=C/F .
1.2. LONGUEUR PHYSIQUE ET LONGUEUR ELECTRIQUE
La longueur physique est la longueur réelle de la ligne, elle se mesure en mètre (m).
La longueur électrique d’une ligne est déterminé par la fréquence de l’énergie transportée et se mesure en longueur d’onde.
1.3. IMPEDANCE CARACTERISTIQUE D’UNE LIGNE INFINIE SANS PERTE
On considère une ligne infinie sans perte. Donc les grandeurs R et G sont négligeables. Toute l’énergie fournie par la self sera égale à l’énergie absorbée par la capacité :
D’où
Donc :
1.4. VITESSE DE PROPAGATION D’UNE LIGNE SANS PERTE
La quantité d’électricité délivrée à la ligne par la batterie de force électromotrice E a pour valeur :
Q = It = CE t=CE/I
D’où t=racin(LC)
Par suite : V=l/racine(LC)
l = longueur de la ligne
1.5. COEFFICIENT DE PROPAGATION
La vitesse de propagation dans un conducteur est inférieure à celle de la lumière dans le vide.
Le cœfficient de propagation est le rapport de la vitesse de propagation dans le conducteur à la célérité de la lumière.
On a lair=C/F et lconducteur= V/F
Donc : g=V/C
D’où : lconducteur= g lair
2. LIGNE FINIE
2.1. ONDES PROGRESSIVES
Lorsqu’une ligne est refermée sur une charge d’impédance égale à son impédance caractéristique, on n’aura que les ondes progressives.
2.2. REFLEXION
Lorsqu’un ligne n’est pas adaptée (l’impédance de la charge et l’impédance caractéristique de la ligne sont différentes), on aura une réflexion c’est-à-dire création d’une onde réfléchie qui revient vers sa source.
2.2.1. LIGNE OUVERTE
La tension est réfléchie avec la même polarité sans modification d’amplitude ni de forme par l’impédance infinie présente à l’extrémité de la ligne Ei = Er .
Le courant est réfléchi avec inversion de polarité sans modification d’amplitude ni de forme Ii =-Ir
2.2.2. LIGNE COURT-CIRCUITEE
La tension est réfléchie avec inversion de polarité sans modification d’amplitude (Er=-Ei ), le courant est réfléchi avec la même polarité et même amplitude ( Ii = Ir).
2.3. ONDES STATIONNAIRES
Ce sont les ondes résultantes de courant et de tension des ondes progressives et des ondes réfléchies.
Lorsqu’une ligne est refermée sur une impédance différente de son impédance caractéristique, la ligne sera le siège d’ondes stationnaires.
2.3.1. CAS DE LA LIGNE OUVERTE
Transparent n° 1 : Représentation conventionnelle des ondes stationnaires
Un nœud de tension apparaît toujours à l/4 de l’extrémité ouverte et d’autres nœuds apparaissent toutes les demi-longueurs d’onde l/2 .
Un ventre de tension apparaît à l’extrémité ouverte et d’autres ventres apparaissent toutes les demi-longueurs d’onde.
Nota :
Raisonnement inverse pour le courant.
2.3.2. CAS DE LA LIGNE COURT-CIRCUITEE
Transparent n° 2 : Représentation conventionnelle des ondes stationnaires
Un nœud de tension apparaît à l’extrémité de la ligne à l/4 et d’autres nœuds apparaissent toutes lesl/2 .
Un ventre de tension apparaît toujours àl/4 de l’extrémité de la ligne et d’autres ventres apparaissent toutes lesl/2 .
Nota :
Raisonnement inverse pour le courant.